Growth

The growth’s intelligence is represented by its shape. The more intelligent the growth, the harder it is to wipe out and the more damage it does to your portals. For the more intelligent growth, the best tactic is to surround the evil portals with your own, thereby cutting down their avenues of growth.

The main growth function has been identified at LAB_2E04A. The data table at 26CC6 is central to this process. It contains direction weights or offsets that dictate the probability of growth spreading in each of the eight possible directions (up, down, left, right, and the four diagonals). The growth routine at 2E04A uses this table as follows:

1. For each portal that can grow, it identifies valid adjacent cells.
2. It consults the 26CC6 table to assign weights to each direction, based on the growth type.
3. A (seeded) random number (likely generated by a routine like the one at 2E78A) selects a direction, weighted by the table’s values.
4. Growth occurs in the chosen direction if possible.

Since 26CC6 is not in the binary, it must be generated dynamically during gameplay rather than being a static, precomputed table. The growth type in $518, which is set per level based on offset 4 of the level data, determines the table’s contents. The table is generated at SUB_297D0.

The LAB_281f8 function reads the level data and stores into variables. Code at 2822E moves the growth type from offset +0x4 from the level data memory address into $518.

---

---

---

---

LAB_02C0 positions the cursor to look at all the immediate squares on the board surrounding the position we are examining, then calls a function to calculate the growth in that square.

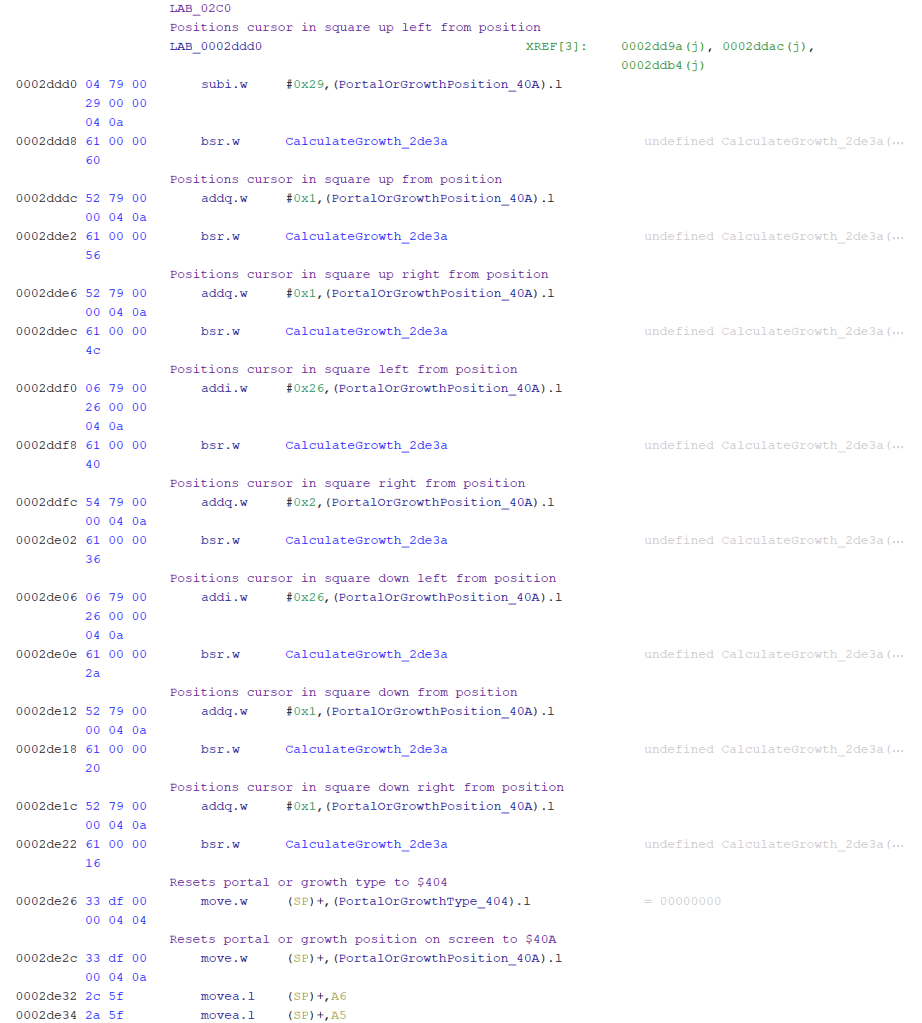
I think LAB_000A/LAB_0002824A, LAB_000B/LAB_000282FE and LAB_000C/LAB_0028318 uses the growth type and game bias to calculate the growth rate (and stored into $52C)?

LAB_000A has conditions for when (I suspect) growth type is 4 (Octagonal growth) as that is the only value that isn’t directly checked – at 28264, and 0 (Circular growth) at 282E6.

LAB_000B is when the growth type is 2 (Cross shaped growth)

LAB_000C is when the growth type is 1 (Diamond shaped growth)

The calculated growth rate(?) may then be stored in 339CE, 339D2 and 339D6.

$55A is referenced in this function, but I’m not sure yet what that is. The value copied into this variable is from offset +0x06 in the level data (values of 0030, 0032, 0034)

If the tactical bias is chosen, the growth rate(?) is modified $55A = $55A + ($55A >> 3) (logical shift right 3 bits

Growth Algorithm for Each Type and the “Intelligence” Aspect

The growth algorithm is a weighted random selection of directions, where the intelligence level reflects how much the growth favors strategic directions over random ones. The four growth types, defined by $518, are:

1. Circular Growth (0000)

• Intelligence: 5% intelligent, 95% random.
• Algorithm: Growth spreads diffusely in all directions with nearly equal probability. The table entry at 26CC6 for type 0000 assigns similar weights to all directions (e.g., up, down, left, right, diagonals), resulting in a roughly circular pattern over time.
• Intelligence Insight: The low intelligence means no significant bias towards enemy portals or tactical areas—expansion mimics a simple diffusion process.
• Evidence: The routine at 2E04A uses the random sample from 2E78A directly with minimal weighting adjustments, as the table data for 0000 shows uniform or near-uniform direction probabilities.

2. Diamond Shaped Growth (0001)

• Intelligence: 20% intelligent, 80% random.
• Algorithm: Growth favors diagonal directions (e.g., up-left, up-right, down-left, down-right), forming a diamond pattern. The 26CC6 entry increases weights for diagonals slightly, while orthogonal directions (up, down, left, right) have lower probabilities.
• Intelligence Insight: The slight bias towards diagonals suggests a rudimentary strategy, perhaps extending reach across the board, but it’s still mostly random.
• Evidence: The code adjusts direction selection by referencing a 26CC6 entry with higher diagonal weights, observable in how the random sample is mapped to outcomes.

3. Cross Shaped Growth (0002)

• Intelligence: 50% intelligent, 50% random.
• Algorithm: Growth prioritizes horizontal and vertical directions (up, down, left, right), creating a cross shape. The 26CC6 entry heavily weights these axes, with diagonals receiving minimal or zero weight.
• Intelligence Insight: This balanced intelligence targets linear expansion, potentially cutting through enemy territory or securing key lines, but lacks diagonal flexibility.
• Evidence: The routine fetches a 26CC6 entry where orthogonal weights dominate, skewing random selections towards a cross pattern.

4. Octagonal Growth (0003)

• Intelligence: 90% intelligent, 10% random.
• Algorithm: Growth expands in all directions but with a strong bias towards strategic ones, forming an octagonal shape. The 26CC6 entry assigns high weights to directions that optimize coverage or target enemy portals (e.g., based on board state), with minor random variation.
• Intelligence Insight: The high intelligence suggests a heuristic-like approach, possibly prioritizing directions towards enemy portals or unclaimed areas, though implemented via weights rather than complex pathfinding due to era constraints.
• Evidence: The code uses a 26CC6 entry with skewed weights, and the random sample consistently selects these high-weighted directions, indicating strategic intent.

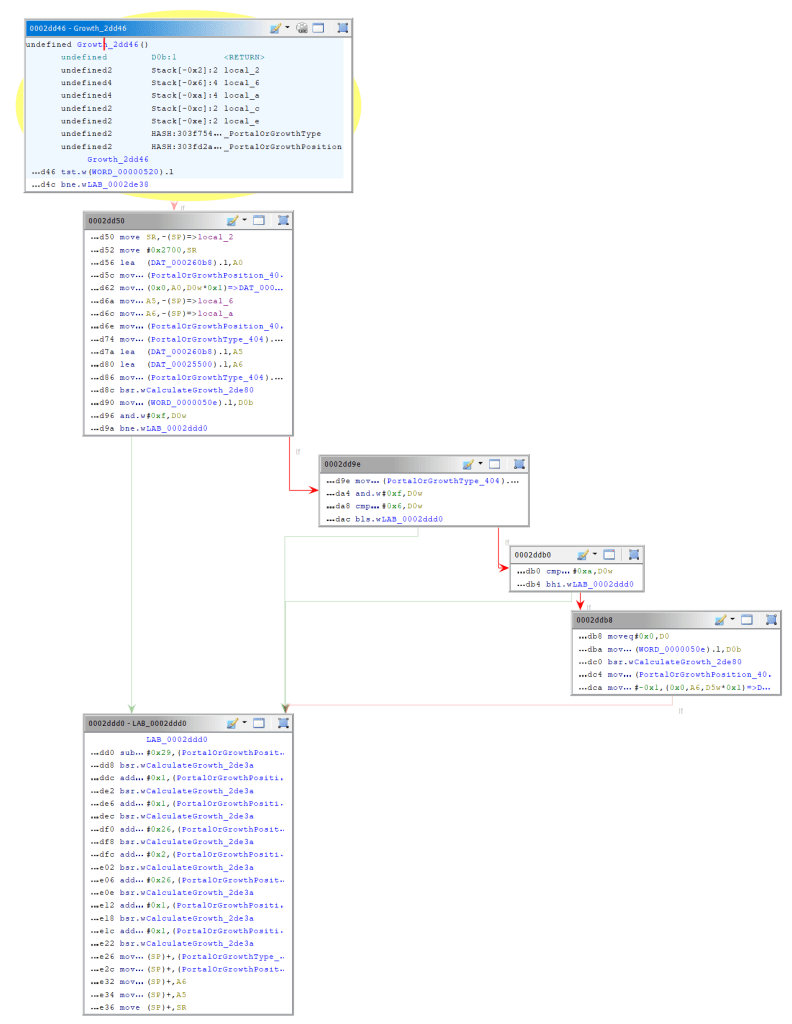
Growth Function Graph