Manhattan Distance

The way growth spreads in Wicked has always fascinated me. Ever since I read that the four types of growth have different ‘intelligences’ in the player’s guides, I’ve wanted to figure out exactly how it works. Now, after digging into the game’s code, I’ve tracked down the growth routine, and with some help from Aira Force, I’ve uncovered and decoded several key tables — finally shedding some light on what’s really going on.

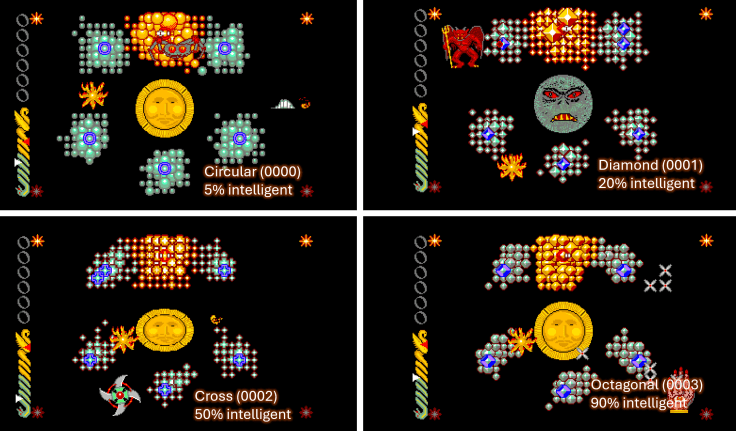
You can see the different “intelligences” in this modified C1S0 level, where the types of portal were reversed in the level data to give us five evil portals and one good portal. The circular (least intelligent) growth is mostly growing outwards in random directions, but the octagonal (most intelligent) is clearly growing towards the one good portal.

The primary subroutine managing growth is located at memory address 2E04A. This routine oversees the expansion of growth across the game board, processing each column (1 to 40) in each row, and determining how growth spreads from each portal. It interacts with several key components:

The growth type is read from the level data into $518, stored as a 16-bit value (0000 to 0003)

Growth Type	$518 Value	Shape	Intelligence (% Intelligent)	Random Growth (%)
Circular Growth	0000	Round	5%	95%
Diamond Shaped Growth	0001	Diamond	20%	80%
Cross Shaped Growth	0002	Cross	50%	50%
Octagonal Growth	0003	Octagonal	90%	10%

2. It checks whether the growth is good or evil in $420 at 2E088. If it is zero (evil growth), the code proceeds to use a pathfinding table at 26CC6 for an intelligent base direction to grow in. If $420 is non-zero (good growth), it branches to 2E0C4, where it just grows randomly.

3. The pathfinding data table at 26CC6: This table contains base direction values that are ‘suggestions’ for growth direction from each portal. It is generated every iteration of the main loop (at 28AC6) by a subroutine at memory address 297D0. It stores a direction (a value from 0 to 3) for each evil portal, indicating the optimal diagonal path toward the closest good portal.

4. It then calls a subroutine at 2E78A, which generates a pseudo-random value. This random value is used to modify the base direction from the data table, introducing a little bit of variability into the growth pattern and determining the final direction in which growth attempts to expand.

Putting it all together
One of the standout findings from digging into the growth mechanics of Wicked is the game’s clever use of Manhattan Distance to steer the spread of evil growth toward good portals and store this information in the pathfinding table at 26CC6. This choice is a perfect match for the game’s grid-based design where the board is a 40-column, 24-row layout, and a testament to the ingenuity of the developers working within the hardware limits of the late 1980s.

What is Manhattan Distance?
Manhattan Distance — sometimes nicknamed “taxicab geometry” — is a way to measure how far apart two points are on a grid when you can only move horizontally or vertically, like a taxi navigating the blocks and city streets in Manhattan. Unlike a straight-line distance, it counts the total number of steps along the grid’s rows and columns.

The formula is simple: for two points, say (row₁, col₁) and (row₂, col₂), the Manhattan Distance is:

Distance = | row₁ - row₂ | + | col₁ - col₂ |

Here:

row is the row number,
col is the column number,
|…| means the absolute value (so the result is always positive).

How It Works in “Wicked”

In Wicked, evil portals don’t grow aimlessly—they target good portals strategically. Manhattan Distance is the key to this behaviour. Here’s the process:

Locate the Portals: The game tracks the positions of all evil and good portals on the board.
Measure Distances: For each evil portal, it calculates the Manhattan Distance to every good portal.
Pick the Closest: The good portal with the smallest distance becomes the target.
Guide the Growth: The game then decides the direction for the evil growth to move toward that target and stores it in the table.

0000: Up-right
0001: Down-right
0002: Down-left
0003: Up-left

This system ensures the evil growth feels purposeful, creeping closer to good portals step by step across the grid.

A Quick Example (using C7S1)

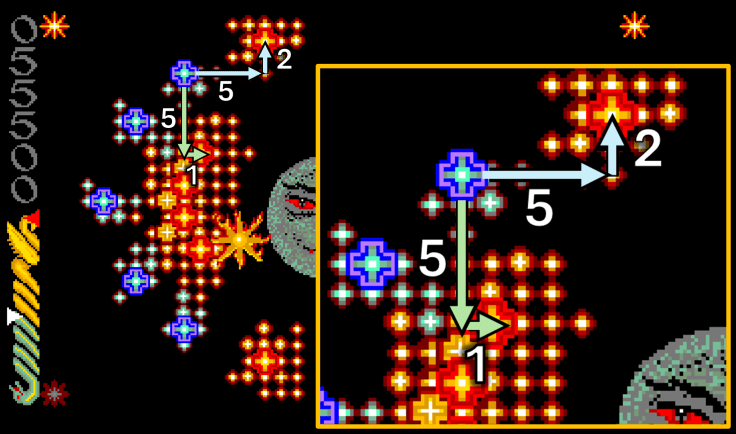
Let’s take the evil portal at (3, 10) and two good portals at (1, 15) and (8, 11):

To (1, 15): ∣ 3 − 1 ∣ + ∣ 10 − 15 ∣ = 2 + 5 = 7
To (8, 11): ∣ 3 − 8 ∣ + ∣ 10 − 11 ∣ = 5 + 1 = 6

The closest good portal is at (8, 11) with a Manhattan Distance of 6. Since this portal is located down and to the right of the evil portal, the evil portal would grow in the down-right direction to approach it, reducing both the row and column differences in a single step.

Why Use Manhattan Distance?

So why did Wicked’s developers choose this over, say, the straight-line (Euclidean) distance? Two big reasons stand out:

Speed: Back in the 16-bit days, computing power was limited. Calculating a straight-line distance involves square roots and floating-point maths — slow and resource-heavy. Manhattan Distance uses just addition and absolute values, making it lightning-fast by comparison.
Grid Fit: Since Wicked’s board is a grid, movement is naturally horizontal or vertical. Manhattan Distance mirrors this, measuring the actual steps needed to reach a target, not an imaginary diagonal shortcut.

Still to do
I’ve not yet uncovered how the different game biases affect the growth in the code.

The Bigger Picture

Uncovering Manhattan Distance in Wicked highlights how the developers blended maths and creativity to craft engaging gameplay under tight constraints, making the evil growth feel smart and relentless. For anyone interested in retro game design, it’s a brilliant peek under the hood at how simple ideas can power complex systems.